Alba Málaga est arrivée le 1^er septembre 2020 au Loria dans l’équipe GAMBLE, commune au CNRS, à Inria et à l’Université de Lorraine, en tant qu’enseignante-chercheuse (maîtresse de conférences) à l’IUT de Saint-Dié. Mathématicienne et conceptrice d’objets mathématiques, elle nous partage ses passionnants projets passés, actuels et futurs.

Qu’est-ce qui vous a amenée à l’illustration mathématique ?

« On peut aujourd’hui faire des dessins et des objets impressionnants sans savoir dessiner ni sculpter, du moment qu’on sait programmer les outils numériques de fabrication, qui se sont démocratisés ces dernières années. C’est ce qui m’a amenée à devenir moi-même créatrice d’images et d’objets mathématiques à une époque où mon domaine de recherche était pourtant tout autre, puisque l’objectif de ma thèse était d’étudier les comportements typiques d’une famille de systèmes dynamiques.

J’ai passé l’année 2019–2020 comme post-doc à l’ICERM (aux États-Unis) dans le cadre du programme spécial Illustrating Mathematics. Ce programme a été le catalyseur de rencontres avec d’autres personnes investies dans la création d’objets et d’images mathématiques. L’esprit de cette démarche a été condensé dans le Manifeste des makers mathématiques que nous avons signé début 2020.

Pour vous donner un exemple, j’ai contribué à un projet de fabrication de papier hyperbolique. Notre objectif était de fabriquer du papier à courbure négative constante, afin de disposer d’un nouveau support illustrant les propriétés du plan hyperbolique. Ce projet a pour ambition d’être utile dans le domaine de l’éducation pour un cours de géométrie notamment.

Ma recherche actuelle s’axe sur la conception d’algorithmes géométriques pour mieux comprendre les objets mathématiques. Plusieurs des problèmes que je traite pour créer des objets mathématiques sont au coeur des préoccupations de recherche de l’équipe GAMBLE : plongements linéaires de tores plats, représentations exactes de surfaces algébriques, triangulations de surfaces hyperboliques. J’anticipe de riches collaborations avec Monique Teillaud et Vincent Despré sur les algorithmes de géométrie non euclidienne, et avec Sylvain Lazard et Guillaume Moroz sur la représentation de surfaces algébriques. Je ne suis pas la seule maker de l’équipe : Laurent Dupont, qui enseigne comme moi en métiers du multimédia et de l’internet, a même ouvert un maker space. »

Quelles sont les applications de votre recherche ?

« C’est principalement via la médiation scientifique que mes recherches s’appliquent. En 2015, j’ai participé à une importante exposition nommée Mathématiques vivantes et visuelles dans le Vieux port de Marseille, organisée par le CIRM et la Chaire Jean-Morlet. Pour ce forum j’ai dû imprimer des objets et j’ai trouvé cela parfait ! Les visiteurs pouvaient ainsi visualiser autrement les mathématiques et plus particulièrement les surfaces algébriques.

En ce moment, je travaille sur un projet de réalisation du globe terrestre en pseudosphère, issu de discussions avec l’équipe mathématique du Palais de la découverte à Paris. Ma surface de travail est à courbure constante négative, ce qui correspond à un modèle de la géométrie hyperbolique. On peut dire que notre planète est une sphère à courbure positive (figure 1), et que la surface sur laquelle j’applique la carte de la Terre est à courbure négative (figure 2). Cette surface a une pointe de longueur infinie, qu’on tronque pour des raisons pratiques.

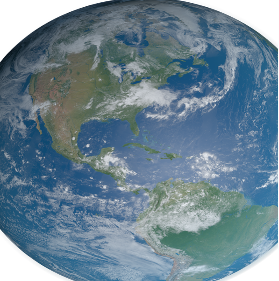
Figure 1

Figure 2

Ce travail permettrait aux visiteurs, et plus particulièrement aux enfants, de manipuler l’objet, ce qui n’est pas toujours possible dans les musées. »

Un petit plus à ajouter ?

« Je suis très contente d’avoir rejoint l’équipe GAMBLE qui m’a chaleureusement accueillie. La vie de laboratoire est très importante pour moi, et elle est très riche dans l’équipe GAMBLE, avec beaucoup d’interactions.

J’ai très envie de visiter le LF2L, le Lorraine Fab Living Lab à Nancy. J’aime beaucoup les fablabs car ce sont des lieux de recherche et d’expérimentation, accessibles à tous les citoyens.

Je vous conseille de lire l’article Folding the hyperbolic crane sur la géométrie hyperbolique si le sujet vous intéresse. N’hésitez pas non plus à parcourir la page des tores plats sur le site MathCurve ou la page du projet Paper flat tori sur le site d’illustration mathématique à l’ICERM. »

• Découvrez tous les projets d’Alba Málaga sur sa page personnelle.
• Plus d’informations sur l’équipe GAMBLE
• En savoir plus sur AuDiMath : réseau autour de la diffusion des mathématiques, regroupant des acteurs du monde universitaire investis dans le développement d’activités de diffusion des mathématiques.